11 Fluid Mechanics
Learning Outcomes
- Explain buoyancy and Archimedes' principle;
- Describe fluid flow and its characteristics (e.g., laminar vs. turbulent flow);
- Analyze the buoyancy and stability of marine organisms and objects;
- Apply Bernoulli’s principle and the continuity equation to fluid flow in marine environments
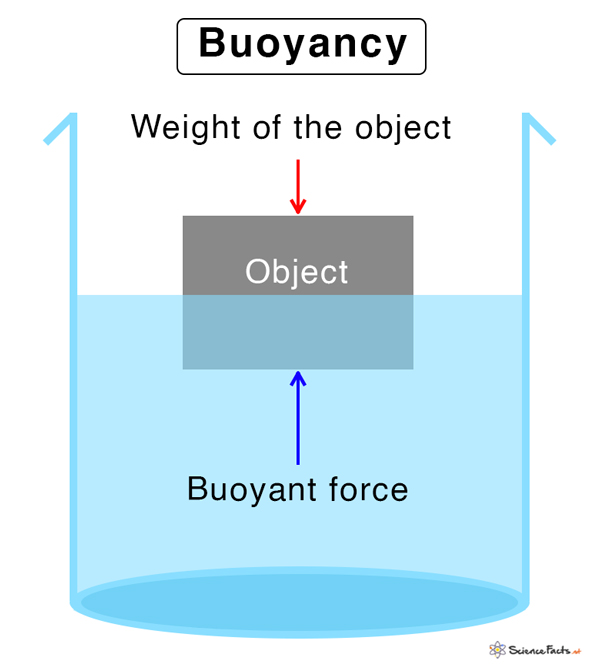
Buoyancy and Archimedes' Principle
Buoyancy is the upward force exerted by a fluid that opposes the weight of an immersed object. This force is crucial for understanding how objects behave in water, particularly in marine biology, where organisms must navigate their buoyancy to survive. Archimedes' Principle states that the buoyant force acting on a submerged object is equal to the weight of the fluid displaced by that object. Mathematically, this can be represented as:
Fb = ρf g Vdisp
where:
- Fb = buoyant force,
- ρf = density of the fluid,
- g = acceleration due to gravity,
- Vdisp = volume of fluid displaced.
This principle explains why objects float or sink, depending on their density relative to the fluid.
Sample Problems
Implications for Marine Biology
Understanding buoyancy and Archimedes' principle is vital for marine biology as it affects how organisms interact with their environment:
- Adaptation Strategies: Many marine organisms have developed adaptations such as swim bladders or specialized body shapes to regulate their buoyancy effectively.
- Ecosystem Dynamics: The buoyancy effects influence nutrient distribution and habitat formation in aquatic ecosystems, impacting food webs and species interactions.
- Research Applications: Knowledge of these principles aids researchers in designing experiments and understanding organism behavior in various marine environments.
In summary, buoyancy and Archimedes' principle are fundamental concepts that not only explain how objects behave in water but also provide insights into ecological dynamics and organism adaptations within marine biology.
Buoyancy and Archimedes' Principle: Problem Set
Problem 1: Buoyant Force on a Fish
A fish has a volume of 0.3 m³ and is swimming in seawater with a density of 1025 kg/m³. Calculate the buoyant force acting on the fish.
Problem 2: Floating Seaweed
A piece of seaweed weighs 10 N in air. When placed in seawater, it weighs 4 N. Determine the buoyant force acting on the seaweed and calculate the volume of seawater displaced.
Problem 3: Submerged Whale
A whale weighs 200,000 N in air. When submerged, it weighs 180,000 N. Calculate the buoyant force acting on the whale and determine the volume of water displaced, assuming seawater density is 1025 kg/m³.
Problem 4: Density of a Jellyfish
A jellyfish has a volume of 0.05 m³ and is observed to float in water. If the jellyfish weighs 30 N, calculate its density and determine if it would float in freshwater (density = 1000 kg/m³).
Problem 5: Sinking Object
An iron anchor weighs 80 N in air and weighs 70 N when submerged in seawater. Calculate the buoyant force acting on the anchor and determine its volume.
Problem 6: Swim Bladder Adjustment
A fish with a swim bladder can adjust its volume from 0.01 m³ to 0.015 m³. If the fish weighs 15 N, calculate how much buoyant force changes when it increases its swim bladder volume.
Problem 7: Coral Reef Structure
A coral structure displaces a volume of water equal to 2 m³ when submerged. Calculate the buoyant force acting on this coral structure if seawater density is 1025 kg/m³.
Problem 8: Marine Mammal Adaptation
A seal has a mass of 150 kg. Calculate the buoyant force acting on it when it is fully submerged in seawater. How much weight would it need to lose to float?
Problem 9: Density Comparison
A plastic bottle with a volume of 0.002 m³ floats in seawater but sinks in freshwater. If its weight is measured at 5 N, calculate its density and discuss why it behaves differently in both fluids.
Problem 10: Underwater Research Submersible
An underwater research submersible displaces water with a total volume of 3 m³ while submerged. If the submersible weighs 5000 N, determine if it will float or sink in seawater (density = 1025 kg/m³). Calculate the net force acting on it.
Fluid Flow
Fluid flow is a fundamental concept in physics and engineering, particularly relevant in marine biology. Fluid flow refers to the movement of fluids (liquids and gases) produced by a pressure gradient, which is the difference in pressure across a surface. This movement can occur in various forms and is influenced by factors such as viscosity, density, and the geometry of the flow path.
It can be categorized into two primary types: laminar flow and turbulent flow. Understanding these types of flow is crucial for studying how fluids interact with marine organisms and ecosystems.
Fluid flow is a fundamental concept in physics and engineering, particularly relevant in marine biology. Fluid flow refers to the movement of fluids (liquids and gases) produced by a pressure gradient, which is the difference in pressure across a surface. This movement can occur in various forms and is influenced by factors such as viscosity, density, and the geometry of the flow path.
It can be categorized into two primary types: laminar flow and turbulent flow. Understanding these types of flow is crucial for studying how fluids interact with marine organisms and ecosystems.
Characteristics of Fluid Flow
Laminar Flow
- Definition: Laminar flow occurs when fluid particles move in parallel layers, with minimal mixing between them. The flow is smooth, orderly, and predictable. In marine biology, laminar flow typically occurs in calm, protected waters, like lagoons. Here, organisms adapted to stable environments thrive without the need for high energy adaptations to counter fluid turbulence.
- Velocity Profile: In laminar flow, the velocity profile is parabolic, with the highest velocity in the center and decreasing towards the edges.
- Reynolds Number: Laminar flow typically occurs at Reynolds numbers (Re) less than 2000. The Reynolds number is calculated as:
Re = ρvD/μ
where:
- ρ = fluid density,
- v = fluid velocity,
- D = characteristic length (e.g., diameter of a pipe),
- μ = dynamic viscosity of the fluid.
- Definition: Laminar flow occurs when fluid particles move in parallel layers, with minimal mixing between them. The flow is smooth, orderly, and predictable. In marine biology, laminar flow typically occurs in calm, protected waters, like lagoons. Here, organisms adapted to stable environments thrive without the need for high energy adaptations to counter fluid turbulence.
- Velocity Profile: In laminar flow, the velocity profile is parabolic, with the highest velocity in the center and decreasing towards the edges.
- Reynolds Number: Laminar flow typically occurs at Reynolds numbers (Re) less than 2000. The Reynolds number is calculated as:
Re = ρvD/μ
where:
- ρ = fluid density,
- v = fluid velocity,
- D = characteristic length (e.g., diameter of a pipe),
- μ = dynamic viscosity of the fluid.
Turbulent Flow
- Definition: Turbulent flow is characterized by chaotic and irregular fluid motion, leading to significant mixing and energy dissipation. In turbulent waters, organisms experience high-energy environments, which enhance nutrient mixing, benefiting primary producers such as phytoplankton. Turbulence supports high biodiversity, as it promotes nutrient-rich conditions essential for marine food webs.
- Velocity Profile: The velocity profile in turbulent flow is flatter compared to laminar flow due to the mixing of layers.
- Reynolds Number: Turbulent flow generally occurs at Reynolds numbers greater than 4000. Between 2000 and 4000, the flow may transition from laminar to turbulent.
- Definition: Turbulent flow is characterized by chaotic and irregular fluid motion, leading to significant mixing and energy dissipation. In turbulent waters, organisms experience high-energy environments, which enhance nutrient mixing, benefiting primary producers such as phytoplankton. Turbulence supports high biodiversity, as it promotes nutrient-rich conditions essential for marine food webs.
- Velocity Profile: The velocity profile in turbulent flow is flatter compared to laminar flow due to the mixing of layers.
- Reynolds Number: Turbulent flow generally occurs at Reynolds numbers greater than 4000. Between 2000 and 4000, the flow may transition from laminar to turbulent.
Sample Problems
Problem 1: Fish Swimming
A fish swims through water at a velocity of 1 m/s. If the water has a density of 1000 kg/m³ and a viscosity of 0.001 Pa·s, determine whether the flow around the fish is laminar or turbulent.
Problem 2: Coral Reef Water Flow
Water flows through a narrow channel formed by coral reefs with a diameter of 0.1 m at a speed of 0.5 m/s. Calculate the Reynolds number and determine the type of flow.
Problem 3: Nutrient Distribution
In a marine environment, water flows over a seagrass bed with an average velocity of 0.2 m/s. If the seagrass has a height of approximately 0.5 m, discuss whether this scenario would likely result in laminar or turbulent flow.
Fluid Flow Problem Set
Problem 1: Fish Swimming
A fish swims through water at a velocity of 2.5 m/s. If the water has a density of 900 kg/m³ and a viscosity of 0.002 Pa·s, determine whether the flow around the fish is laminar or turbulent.
Problem 2: Coral Reef Water Flow
Water flows through a narrow channel formed by coral reefs with a diameter of 0.4 m at a speed of 0.5 m/s. Calculate the Reynolds number and determine the type of flow.
Problem 3: Nutrient Distribution
In a marine environment, water flows over a seagrass bed with an average velocity of 0.7 m/s. If the seagrass has a height of approximately 1.5 m, discuss whether this scenario would likely result in laminar or turbulent flow.
Problem 4: Jellyfish Propulsion
A jellyfish propels itself by contracting its bell, creating a jet of water that moves at a speed of 2 m/s through seawater (density = 1025 kg/m³, viscosity = 0.001 Pa·s). Calculate the Reynolds number for this jet and determine the nature of the flow.
Problem 5: Sediment Transport
A river flows with an average velocity of 3 m/s through a wide channel (width = 10 m). If the river's depth is about 2 m, calculate the Reynolds number and analyze whether sediment transport will be affected by laminar or turbulent conditions.
Problem 6: Blood Flow in Marine Mammals
The blood flowing through the arteries of a dolphin has a viscosity of about 0.004 Pa·s and flows at an average speed of 1 m/s through arteries with a diameter of 0.02 m. Determine if this blood flow is laminar or turbulent.
Problem 7: Plankton Movement
Plankton are often suspended in water where currents are present. If the average current velocity is measured at 0.1 m/s in an area with a depth of approximately 1 m, calculate whether this movement will create laminar or turbulent conditions based on typical water properties.
Problem 8: Wave Action on Shorelines
Waves crashing onto a shoreline create complex fluid dynamics. If wave heights reach up to 2 m and travel at speeds of about 5 m/s, discuss how these conditions might affect sediment transport due to turbulence.
Problem 9: Fish Schooling Behavior
Consider a school of fish swimming together at an average speed of 1.5 m/s in seawater (density = 1025 kg/m³). Calculate the Reynolds number for their schooling behavior if they swim closely together with an average body diameter of about 0.1 m.
Problem 10: Aquatic Plant Growth
An aquatic plant has roots that extend into sediment while its leaves float on water's surface. If water flows over these plants at a speed of approximately 0.3 m/s, analyze whether this scenario promotes laminar or turbulent flow around the plant structure based on its height and surrounding conditions.
Problem 1: Fish Swimming
A fish swims through water at a velocity of 2.5 m/s. If the water has a density of 900 kg/m³ and a viscosity of 0.002 Pa·s, determine whether the flow around the fish is laminar or turbulent.
Problem 2: Coral Reef Water Flow
Water flows through a narrow channel formed by coral reefs with a diameter of 0.4 m at a speed of 0.5 m/s. Calculate the Reynolds number and determine the type of flow.
Problem 3: Nutrient Distribution
In a marine environment, water flows over a seagrass bed with an average velocity of 0.7 m/s. If the seagrass has a height of approximately 1.5 m, discuss whether this scenario would likely result in laminar or turbulent flow.
Problem 4: Jellyfish Propulsion
A jellyfish propels itself by contracting its bell, creating a jet of water that moves at a speed of 2 m/s through seawater (density = 1025 kg/m³, viscosity = 0.001 Pa·s). Calculate the Reynolds number for this jet and determine the nature of the flow.
Problem 5: Sediment Transport
A river flows with an average velocity of 3 m/s through a wide channel (width = 10 m). If the river's depth is about 2 m, calculate the Reynolds number and analyze whether sediment transport will be affected by laminar or turbulent conditions.
Problem 6: Blood Flow in Marine Mammals
The blood flowing through the arteries of a dolphin has a viscosity of about 0.004 Pa·s and flows at an average speed of 1 m/s through arteries with a diameter of 0.02 m. Determine if this blood flow is laminar or turbulent.
Problem 7: Plankton Movement
Plankton are often suspended in water where currents are present. If the average current velocity is measured at 0.1 m/s in an area with a depth of approximately 1 m, calculate whether this movement will create laminar or turbulent conditions based on typical water properties.
Problem 8: Wave Action on Shorelines
Waves crashing onto a shoreline create complex fluid dynamics. If wave heights reach up to 2 m and travel at speeds of about 5 m/s, discuss how these conditions might affect sediment transport due to turbulence.
Problem 9: Fish Schooling Behavior
Consider a school of fish swimming together at an average speed of 1.5 m/s in seawater (density = 1025 kg/m³). Calculate the Reynolds number for their schooling behavior if they swim closely together with an average body diameter of about 0.1 m.
Problem 10: Aquatic Plant Growth
An aquatic plant has roots that extend into sediment while its leaves float on water's surface. If water flows over these plants at a speed of approximately 0.3 m/s, analyze whether this scenario promotes laminar or turbulent flow around the plant structure based on its height and surrounding conditions.
Bernoulli's Principle
Bernoulli's Principle states that within a flowing fluid, an increase in fluid speed occurs simultaneously with a decrease in pressure or potential energy. Bernoulli's Principle is observed in how water flows around organisms and objects. For instance, water speed increases over fish bodies with streamlined shapes, reducing pressure and lowering drag, allowing fish to move efficiently. This principle can be expressed mathematically as:
P + (1/2)ρv2 + ρgh = constant
where:
- P = pressure,
- ρ = fluid density,
- v = fluid velocity,
- g = acceleration due to gravity,
- h = height above a reference level.
This equation implies that in regions where fluid velocity increases (e.g., through constrictions), pressure decreases. This principle is crucial for understanding various phenomena in marine environments.
Bernoulli's Principle states that within a flowing fluid, an increase in fluid speed occurs simultaneously with a decrease in pressure or potential energy. Bernoulli's Principle is observed in how water flows around organisms and objects. For instance, water speed increases over fish bodies with streamlined shapes, reducing pressure and lowering drag, allowing fish to move efficiently. This principle can be expressed mathematically as:
P + (1/2)ρv2 + ρgh = constant
where:
- P = pressure,
- ρ = fluid density,
- v = fluid velocity,
- g = acceleration due to gravity,
- h = height above a reference level.
This equation implies that in regions where fluid velocity increases (e.g., through constrictions), pressure decreases. This principle is crucial for understanding various phenomena in marine environments.
Continuity Equation
The Continuity Equation states that for an incompressible fluid, the mass flow rate must remain constant from one cross-section of a pipe or channel to another. It can be expressed as:
A1v1 = A2v2
where:
- A = cross-sectional area,
- v = fluid velocity.
This equation indicates that if a fluid flows through a pipe that narrows (reducing area), its velocity must increase to maintain a constant flow rate. In marine environments, this equation helps explain water flow through various underwater structures, like coral reefs, where channel constriction increases water speed, affecting sediment and nutrient transport.
The Continuity Equation states that for an incompressible fluid, the mass flow rate must remain constant from one cross-section of a pipe or channel to another. It can be expressed as:
A1v1 = A2v2
where:
- A = cross-sectional area,
- v = fluid velocity.
This equation indicates that if a fluid flows through a pipe that narrows (reducing area), its velocity must increase to maintain a constant flow rate. In marine environments, this equation helps explain water flow through various underwater structures, like coral reefs, where channel constriction increases water speed, affecting sediment and nutrient transport.
Applications in Marine Environments
- Water Flow Around Marine Structures:
- Understanding how water flows around ships and underwater structures helps engineers design vessels that minimize drag and improve fuel efficiency. The principles behind ship squat (the phenomenon where a ship sinks lower into the water as it moves faster) are directly related to Bernoulli’s principle.
- Nutrient Transport:
- In marine ecosystems, the principles of fluid dynamics facilitate nutrient transport through currents. Turbulent flow can enhance mixing, distributing nutrients more evenly across different depths, which is critical for primary productivity.
- Behavioral Adaptations:
- Many marine organisms have adapted their shapes and swimming techniques based on principles of fluid dynamics. For example, streamlined bodies reduce drag during swimming, allowing for more efficient movement through turbulent waters.
- Ecological Impacts:
- Changes in water flow due to human activities (like damming rivers or coastal development) can disrupt natural sediment transport and nutrient cycling processes essential for maintaining healthy marine ecosystems.
In summary, buoyancy and fluid dynamics play pivotal roles in marine biology by influencing organism behavior, ecological interactions, and environmental adaptations. Understanding these principles allows researchers to better comprehend marine ecosystems' complexities and dynamics.
- Water Flow Around Marine Structures:
- Understanding how water flows around ships and underwater structures helps engineers design vessels that minimize drag and improve fuel efficiency. The principles behind ship squat (the phenomenon where a ship sinks lower into the water as it moves faster) are directly related to Bernoulli’s principle.
- Nutrient Transport:
- In marine ecosystems, the principles of fluid dynamics facilitate nutrient transport through currents. Turbulent flow can enhance mixing, distributing nutrients more evenly across different depths, which is critical for primary productivity.
- Behavioral Adaptations:
- Many marine organisms have adapted their shapes and swimming techniques based on principles of fluid dynamics. For example, streamlined bodies reduce drag during swimming, allowing for more efficient movement through turbulent waters.
- Ecological Impacts:
- Changes in water flow due to human activities (like damming rivers or coastal development) can disrupt natural sediment transport and nutrient cycling processes essential for maintaining healthy marine ecosystems.
In summary, buoyancy and fluid dynamics play pivotal roles in marine biology by influencing organism behavior, ecological interactions, and environmental adaptations. Understanding these principles allows researchers to better comprehend marine ecosystems' complexities and dynamics.





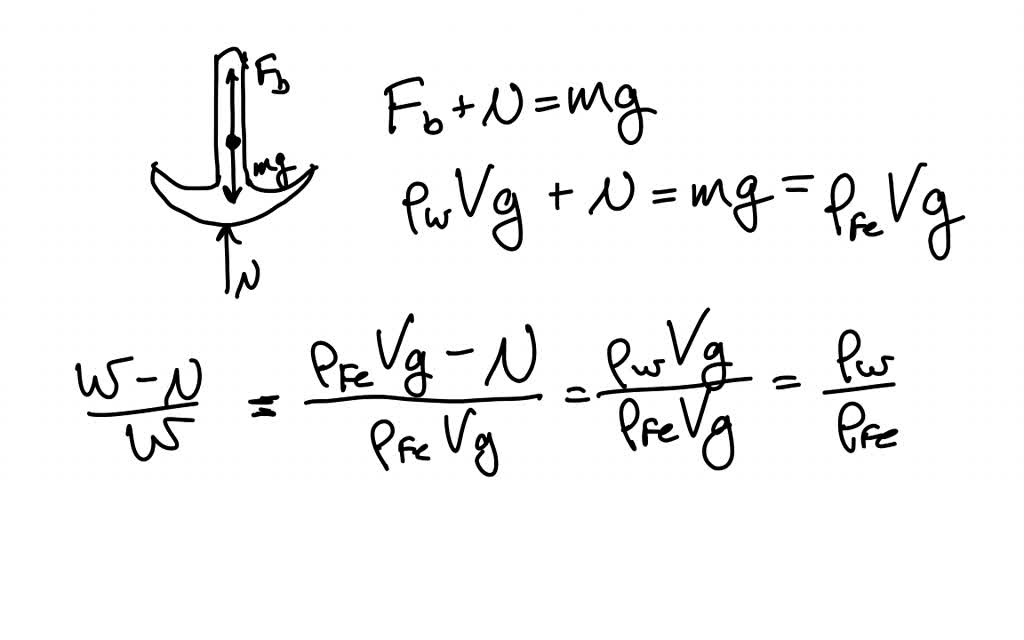







.png)
.png)
.png)
Comments
Post a Comment