03 Simple Vector Addition

 

Differentiating Vector and Scalar Quantities

In physics, we deal with various quantities that describe the properties of objects and the phenomena around us. A quantity is something that can be measured, such as length, mass, time, or speed. However, not all quantities are the same. Some are simple and straightforward, while others carry more information, such as direction. Understanding the difference between these types of quantities is crucial, especially in fields like marine biology, where accurate measurements are essential.

Scalar Quantities

Scalar quantities are those that are described by a magnitude (a numerical value) alone. They do not have direction. For instance, if we say the water temperature is 20°C, we are only giving a magnitude. The temperature is the same regardless of the direction in which it is measured. Other examples of scalar quantities include mass (e.g., 5 kg), time (e.g., 10 seconds), and speed (e.g., 30 km/h). Scalars are often the simplest measurements we can make because they involve only a single piece of information.

Vector Quantities

Vector quantities, on the other hand, have both magnitude and direction. They are used when the direction of the quantity matters in addition to its size. For example, if a fish swims 5 meters to the north, both the distance (5 meters) and the direction (north) are necessary to fully describe its motion. This combination of magnitude and direction makes it a vector quantity. Other examples of vectors include velocity (e.g., 10 km/h east), force (e.g., 15 N downward), and displacement (e.g., 2 meters southeast). In physics, vectors are often represented by arrows, where the length of the arrow indicates the magnitude, and the arrow points in the direction.

Why the Difference Matters

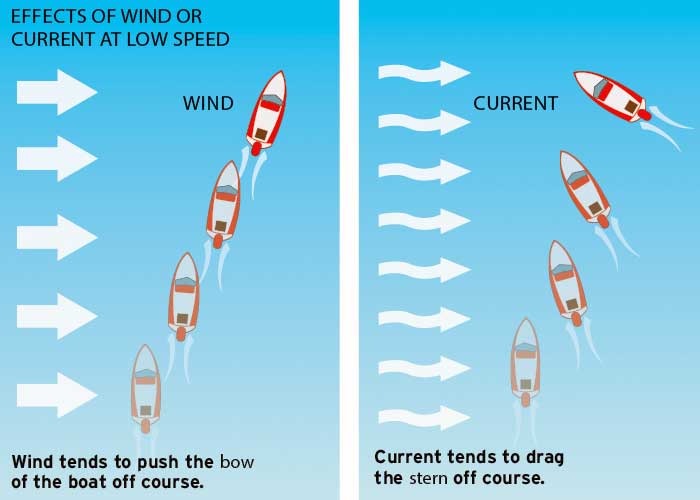
Understanding whether a quantity is a scalar or a vector is important because it affects how we analyze and interpret physical situations. For example, when navigating at sea, knowing the direction of the current (a vector quantity) is just as important as knowing its speed. If only the speed (a scalar quantity) is known, one might not end up where intended.

Classifying Quantities

Now that you understand the difference, let’s practice classifying some quantities. Think about the quantities you encounter in your studies or everyday life. Is weight a vector or a scalar? What about distance or acceleration? Try to classify each one and then discuss your thoughts with a partner. The more you practice, the more intuitive it will become to recognize vector and scalar quantities.

Understanding these concepts will serve as a foundation for more advanced topics in physics and help you better analyze real-world situations in marine biology. If you have any questions or need further clarification, don’t hesitate to ask.

Marine biologists need to understand vector addition to navigate safely when conducting research in open seas.

Adding Vectors Graphically

In marine biology, vector quantities such as ocean currents, wind speed, and the movement of marine organisms are important when studying their behavior and interactions with the environment. Understanding how to add vectors graphically can help visualize these forces and determine the resultant effect, such as the actual path of a fish swimming in a current or the direction a boat will drift due to wind and tide.

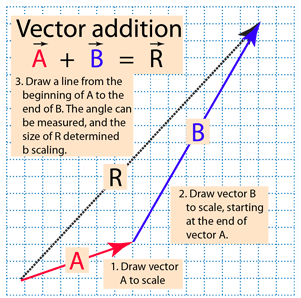
Graphical vector addition, a method used to combine two or more vectors to find a resultant vector. Imagine you are tracking the movement of a marine animal, such as a sea turtle swimming with the current. The turtle's swimming direction and the current's flow are vectors that can be added to find the actual path of the turtle.

Steps to Add Vectors Graphically

1. Determine the Scale: Before drawing, establish a scale to represent the magnitudes of the vectors. For example, 1 cm on paper could equal 1 m/s in real life. This ensures that the vectors are accurately represented according to their true magnitudes.
2. Draw the First Vector (Vector A): Begin by selecting a starting point on the coordinate plane. Draw the first vector according to its magnitude and direction. The length of the arrow should match the magnitude, and the arrow should point in the direction specified (e.g., north-east for the turtle’s swimming direction).
3. Draw the Second Vector (Vector B): Next, from the terminal (end) point of the first vector, draw the second vector according to its magnitude and direction. If this vector represents the ocean current, its direction and length will depict the flow of water.
4. Complete the Resultant Vector: Now, draw a new vector from the initial point of the first vector to the terminal point of the second vector. This new vector is called the resultant vector and represents the combination of the two vectors (e.g., the actual path the turtle will follow).
5. Measure the Resultant Vector: Using a ruler, measure the length of the resultant vector and convert it back to real-world units using the scale. This will give you the magnitude of the resultant vector (e.g., the speed of the turtle relative to the water and current).
6. Determine the Direction of the Resultant Vector: Use a protractor to measure the angle between the resultant vector and a reference axis (typically the x-axis). This angle tells you the direction of the turtle's path relative to a fixed direction like east or north.
7. Express the Resultant Vector: Once you have both the magnitude and the direction, express the resultant vector in terms of its magnitude and angle (e.g., “The turtle's path is 2.5 m/s at an angle of 30° north of east”).

Benefits of the Graphical Method in Marine Biology

The graphical method provides a visual tool for understanding vector relationships. For example, by adding vectors representing wind and ocean currents, marine biologists can estimate the actual movement of floating organisms or debris. The method is valuable when qualitative assessments are needed, such as understanding how different environmental forces combine.

However, the accuracy of the graphical method depends on factors like the precision of your scale, the quality of your drawing, and the accuracy of your measuring tools. While it may not be as precise as algebraic methods for detailed calculations, it provides an intuitive way to explore vector addition.

Navigating a submersible, especially for marine biology research, requires knowledge of ocean currents and vector addition.

Algebraic Vector Addition

In earlier lessons, you learned how to add vectors graphically, which involve drawing the vectors to scale and finding the resultant vector (the total effect of the combined vectors). The resultant vector is the vector that represents the total effect of all the vectors that have been added together.

However, in more complex cases—such as when vectors are not aligned along standard directions or when multiple vectors are involved—adding vectors graphically can be less practical. This is where algebraic vector addition becomes particularly useful.

Algebraic vector addition allows us to calculate the resultant vector using components. Each vector can be broken down into two parts: a horizontal component along the x-axis and a vertical component.. along the y-axis. These components represent the influence of the vector in the respective directions.

To add vectors algebraically, we'll break them down into their horizontal and vertical components. Then, we can add the corresponding components separately. Finally, we combine the components to obtain the resultant vector.

Given a vector v with magnitude m and direction θ:

1. Find the horizontal component of the vector: vₓ = m * cos(θ)
2. Find the vertical component of the vector: vᵧ = m * sin(θ)
3. Write the vector in component form: v = vₓi + vᵧj, where i and j are unit vectors along the x and y axes, respectively.

By resolving the magnitude of a vector into its horizontal and vertical components, you can represent the vector in its component form. This form is useful for algebraic operations such as vector addition and subtraction, as well as for analyzing vector quantities in different directions.

To add two vectors v₁ and v₂ algebraically, follow these steps:

1. Find the horizontal components of the vectors: vₓ₁ = m * cos(θ); vₓ₂ = m * cos(θ)
2. Find the vertical components of the vectors: vᵧ₁ = m * sin(θ); vᵧ₂ = m * sin(θ)
3. Add the horizontal components: vₓ = vₓ₁ + vₓ₂
4. Add the vertical components: v_y = v_y1 + v_y2
5. Write the sum of the vectors in component form: v = vₓi + vᵧj
6. Find the magnitude m of the resultant vector v using the Pythagorean theorem: m = √(vₓ² + v_y²)
7. Find the direction θ using the inverse tangent function: θ = tan^-1(v_y/vₓ)

By algebraically adding the horizontal and vertical components separately, you can find the resultant vector of the addition operation. This method allows for precise calculations and is particularly useful when dealing with multiple vectors or vectors in non-standard directions.

Example:

A sea turtle's velocity is affected by its own swimming speed and the ocean current.

A marine biologist is tracking the movement of a sea turtle swimming in an ocean current. The ocean current is flowing at a speed of 10 mph from the east. The turtle is swimming at a speed of 5 mph in a direction of 30 degrees north of east. Calculate the resultant velocity vector of the sea turtle, taking into account the effect of the ocean current.

• List the given values: v₁ = 10 mph; v₂ = 5 mph, 30⁰ N of E
• Identify the unknown quantity: v_R = ?
• Find the horizontal components of the vectors: vₓ₁ = 10 * cos(0) = 10; vₓ₂ = 5 * cos(30) = 4.33
• Find the vertical components of the vectors: vᵧ₁ = 10 * sin(0) = 0; vᵧ₂ = 5 * sin(30) = 2.5
• Add the horizontal components: vₓ = vₓ₁ + vₓ₂ = 10 + 4.33 = 14.33
• Add the vertical components: v_y = v_y1 + v_y2 = 0 + 2.5 = 2.5
• Write the sum of the vectors in component form: v = vₓi + vᵧj = 14.33 i + 2.5 j
• Find the magnitude m of the resultant vector v using the Pythagorean theorem: m = √(vₓ² + v_y²) = √(14.3² + 2.5²) = 14.5
• Find the direction θ using the inverse tangent function: θ = tan^-1(v_y/vₓ) = 9.9⁰ north of east

Therefore, the resultant vector of the turtle's velocity, taking into account the effect of the ocean current, is 14.5 mph 9.9⁰ north of east.