06 Newton's Laws of Motion

 

Newton's Laws of Motion

Sir Isaac Newton’s laws of motion are foundational principles in physics that describe the relationship between the motion of an object and the forces acting upon it. For marine biology students, these laws provide essential insights into the behavior of marine organisms and vehicles in aquatic environments. Understanding Newton's three laws of motion can help explain how marine life navigates through water and how human-engineered vessels operate effectively in this unique medium.

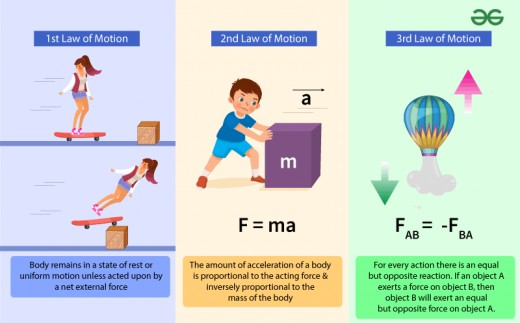
First Law: Law of Inertia

Newton's First Law, often referred to as the Law of Inertia, states that an object at rest will remain at rest, and an object in uniform motion will continue to move in a straight line unless acted upon by a net external force. This principle is particularly relevant in marine environments, where the natural state of marine organisms or vessels is influenced by various external forces.

For instance, a fish swimming steadily in a straight line will continue to do so until it encounters resistance from water currents or changes direction to evade a predator. Similarly, a boat floating on the surface of the water will remain at rest until a force, such as wind or engine thrust, acts upon it. Understanding this law helps marine biology students appreciate the dynamics of movement in water, where factors like buoyancy and water resistance are constantly at play, altering the state of motion for both living creatures and vessels.

Second Law: F = ma

Newton's Second Law of Motion (Law of Acceleration) states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration, expressed mathematically as:

a = F/m → F = m a

This law is crucial for understanding the forces that act on marine organisms and vehicles. For example, when a fish accelerates to catch prey, the force exerted by its muscles propels it forward, overcoming the drag force exerted by the water. The drag force is the resistance that water exerts on a moving object, which must be considered when analyzing the fish's movement.

Additionally, buoyancy plays a significant role in aquatic motion. This upward force, which acts opposite to gravity, allows marine organisms like jellyfish and whales to maintain their position in the water column. When calculating the net force on a marine vehicle, students must also consider thrust—the force generated by the engine to propel the vessel forward. By applying Newton's Second Law, students can analyze how these forces interact to cause acceleration or deceleration in water.

Third Law: Action and Reaction

Newton's Third Law of Motion (Law of Action and Reaction) states that for every action, there is an equal and opposite reaction. This principle is vital for understanding propulsion in marine vehicles and the movement of marine organisms. When a fish uses its fins to push water backward, it generates a reaction force that propels the fish forward. This action-reaction pair is fundamental to the locomotion of many aquatic animals, enabling them to navigate efficiently through their environment.

For marine vehicles, this law is equally important. When a boat's engine produces thrust by expelling water backwards, the reaction force pushes the boat forward. Understanding this interaction allows engineers and marine biologists alike to design more efficient vessels and study the swimming mechanics of marine life.

Newton's laws of motion provide a comprehensive framework for understanding the dynamics of movement in aquatic environments. By applying these principles, marine biology students can gain valuable insights into the behavior of both marine organisms and human-engineered vessels, enhancing their understanding of life in the ocean and the physical forces that shape it.

Problem Set: Laws of Motion and Kinematic Equations

Answer the following problems by listing the given/known values, identifying the unknown quantity, and showing your complete solution.

1. A fish with a mass of 2 kg is swimming in a straight line at a constant velocity of 1 m/s. Suddenly, it encounters a current that exerts a net force of 3 N against its direction of motion. (a) What is the acceleration of the fish due to the current? (b) If the force of the current continues to act, how much time will it take for the fish to come to a stop?
2. A small research submarine with a mass of 5,000 kg is moving horizontally at a speed of 3 m/s. The engine generates a forward thrust of 12,000 N, but the submarine experiences a drag force of 8,000 N from the water. (a) What is the net force acting on the submarine? (b) What is the acceleration of the submarine? (c) If the submarine starts at this speed, how fast will it be moving after 10 seconds?

Kinematics and Newton’s laws are used to model how marine organisms and vehicles are affected by ocean currents and waves, which are important for understanding migration patterns, energy expenditure, and environmental impacts.