01 Introduction to Physics and Measurement

Understanding the physical principles that govern our world is essential for comprehending the complex interactions within marine environments and organisms.

In this reading selection, you will explore the foundational concepts of physics that are crucial for marine biology. You will learn how to use and convert between standard units of measurement in physics (SI units), and how to apply scientific notation to express both large and small quantities efficiently.

By mastering these principles, you will gain a deeper appreciation of how physics helps in the study of marine biology, paving the way for your future explorations in this fascinating field.

Learning Outcomes

• Describe how physical principles help in understanding marine environments and organisms;
• Identify and use standard units of measurement in physics (SI units);
• Convert between different units of measurement; and
• Apply scientific notation in expressing large and small quantities.

The Importance of Units in Marine Biology

Marine biologists, like other scientists, make observations and ask fundamental questions about the ocean and its inhabitants. For example, how large is a particular marine organism? How much does it weigh? How far has it migrated? To answer these questions, they make measurements using various instruments such as measuring tapes, scales, and tracking devices.

The measurements of these physical quantities are expressed in terms of units, which are standardized values. For instance, the size of a fish can be expressed in centimeters, and the distance a turtle migrates can be measured in kilometers. Without standardized units, it would be extremely difficult for marine biologists to express and compare their findings in a meaningful way. This standardization ensures that data is consistent, accurate, and comparable across different studies and regions, facilitating a better understanding of marine life and ecosystems.

Marine biologists measure the size of corals to determine the health of the reef.

SI Units: Fundamental and Derived Units

In marine biology, as in other sciences, some physical quantities must be defined through a measurement process. These are known as base quantities, and their units are the base units of the measurement system. All other physical quantities can then be expressed as algebraic combinations of these base quantities, known as derived quantities, with their units called derived units. The choice of base quantities is somewhat arbitrary as long as they are independent of each other and all other quantities can be derived from them. Typically, base quantities are chosen for their ability to be measured accurately and precisely.

To standardize measurements across various scientific fields, including marine biology, the International Standards Organization recommends seven base quantities, forming the International System of Quantities (ISQ). These base quantities are used to define the SI base units, ensuring consistency and precision in measurements. This standardization is crucial in marine biology for accurate data collection and comparison. (Table 1) lists these seven ISQ base quantities and the corresponding SI base units.

Quantity	Name	Symbol
Length	meter	m
Mass	kilogram	kg
Time	second	s
Electric current	ampere	A
Temperature	kelvin	K
Amount of substance	mole	mol
Luminous intensity	candela	cd

Meter

The meter is defined as the distance light travels in a vacuum in 1/ 299,792,458 of a second (1983).

Second

The second is defined by taking the fixed numerical value of the cesium frequency ΔνCs, the unperturbed ground-state hyperfine transition frequency of the cesium-133 atom, to be 9,192,631,770 when expressed in the unit Hz, which is equal to s⁻¹ (1967). Essentially, this means that a second is defined by the number of vibrations of a cesium atom under specific conditions.

Kilogram

The kilogram (kg) is currently defined using the Planck constant (h), which is a fundamental constant in quantum mechanics. The definition is precise and connects the kilogram to other fundamental constants and units of measurement. As of May 20, 2019, the kilogram is defined by fixing the numerical value of the Planck constant to exactly 6.62607015 × 10⁻³⁴ joule seconds (J·s), where the joule is defined in terms of the meter, kilogram, and second. This means the kilogram is defined based on the second and the meter, with the Planck constant providing the link. This redefinition ensures that the kilogram is tied to unchanging fundamental properties of nature rather than a physical object, thereby improving accuracy and stability in measurement.

The Ampere

Amperes (A) measure electric flow, named after Andre Ampere. One ampere is the amount of electricity that makes two wires pull on each other with a force of 2.7×10^–7 newton per meter when placed apart.

Kelvins

The SI unit of temperature is the kelvin (K), not degrees kelvin. The Kelvin scale is named after physicist William Thomson, Lord Kelvin. It starts at absolute zero, the coldest possible temperature where all thermal energy is gone. Absolute zero is 0 K, which equals −273.15 °C or −459.67 °F. The Kelvin scale changes the same way as the Celsius scale. For example, the freezing point of water is 0 °C (273.15 K) and the boiling point is 100 °C (373.15 K). These points are 100 degrees or kelvins apart.

A marine biologist collecting water samples and recording measurements.

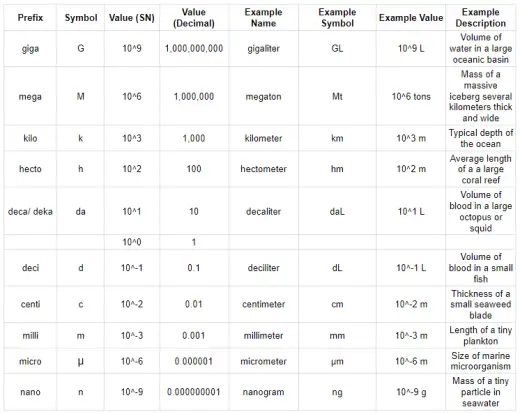
Metric Prefixes

Metric prefixes help measure big and small things. These are standardized multipliers that modify the base unit of a measurement, indicating multiples or submultiples of that unit by powers of ten. These words go before a unit (like meter or gram) to show how big or small something is. They are based on numbers like 10, 100, 1,000, and so on.

Scientific Notation

Scientific notation helps us write very large or very small numbers easily. For example, instead of writing 840,000,000,000,000, we use scientific notation: 8.4 × 10¹⁴. It is a method of writing very large or very small numbers in a simplified form. It expresses numbers as a product of two factors:

x × 10^y

Here, x is the main number with all extra zeros removed. In 8.4 × 10¹⁴, x is 8.4. The 10^y part tells us how many places to move the decimal point. In 8.4 × 10¹⁴, we move the decimal point 14 places to the right to get 840,000,000,000,000.

For very small numbers, like 0.0000045, we also use scientific notation. This number becomes 4.5 × 10^-6. The negative exponent means we move the decimal point to the left. So, for 4.5 × 10^-6, we move the decimal point 6 places to the left to get 0.0000045.

The term order of magnitude refers to the power of 10. Numbers with the same power of 10 are of the same order of magnitude. For example, 800 (8 × 10²) and 450 (4.5 × 10²) have the same power of 10, so they are of the same order of magnitude.

Scientists use scientific notation often because it helps us manage the wide range of measurements found in nature. In marine biology, for example, we measure tiny things like the size of marine microorganisms (around 1 × 10^-6 meters) and huge things like the depth of the ocean (about 1 × 10⁴ meters). Using scientific notation makes it easier to work with these very small and very large numbers, helping marine biologists understand and communicate their research more effectively.

Marine biologist Milton Love researches fish from a manned submersible. 

Conversion of Units

Unit conversions are crucial in marine biology for ensuring accurate data collection and analysis. For instance, when comparing the sizes of marine organisms or the volumes of water samples, consistent units are necessary for valid comparisons and conclusions. Understanding these conversions allows marine biologists to communicate their findings effectively across different scientific communities, which may use varying measurement systems.

Here are some key points and examples on how to perform unit conversions effectively:

1. Identify the Units: Determine the units you are starting with and the units you need to convert to. Common conversions in marine biology include:
   • Length: meters (m) to centimeters (cm) or millimeters (mm)
   • Volume: liters (L) to milliliters (mL)
   • Mass: grams (g) to kilograms (kg)
2. Use Conversion Factors: A conversion factoris a ratio that expresses how many of one unit are equal to another unit. For example:
   • 1 meter=100 centimeters
   • 1 liter=1,000 milliliters1 liter=1,000 milliliters
   • 1 kilogram=1,000 grams1 kilogram=1,000 grams
3. Perform the Calculation:
• To convert larger to smaller units: Multiply by the conversion factor.
• To convert smaller to larger Units: Divide by the conversion factor.

Problem Set

I. Solve the following problems. List the given values and identify the unknown value you need to find. Show the solution step by step.

1. Depth Measurements: Marine biologists often measure depth in meters (m), but in certain contexts, such as scuba diving or fishing, feet may be used. Converting meters to feet (1 m = 3.28084 ft) is necessary for clear communication of depth data. How deep is 100 feet in meters?

2. Fish Length: When documenting the size of marine species, lengths may be recorded in centimeters (cm) or inches. For example, convert a fish length of 30 cm to inches by using the conversion factor 1 inch = 2.54 cm.
3. Volume of Water Samples: Marine biologists frequently collect water samples, measured in liters (L) or milliliters (mL). A study reports water volume in mL, but the researcher collects samples in L. How would a 2.5 L sample be reported in mL?
4. Area Measurements: When studying habitats, area may be measured in square meters (m²) or hectares (ha). Convert from 500 m² to ha (1 ha = 10,000 m²).

References

• Urone, P. P., & Hinrichs, R. (2020). The language of physics: Physical quantities and units. In Physics. OpenStax. https://openstax.org/books/physics/pages/1-3-the-language-of-physics-physical-quantities-and-units